[혼자 공부하는 머신러닝+딥러닝] 20강. 합성곱 신경망의 개념과 동작 원리 배우기 - 2차원 이미지를 그대로 학습 해보자!
https://www.youtube.com/watch?v=tPLRox0YYc8&list=PLJN246lAkhQjoU0C4v8FgtbjOIXxSs_4Q&index=21
- 밀집층
- 기존 학습의 방법은 밀집층(dense)를 이용해 학습을 했다.
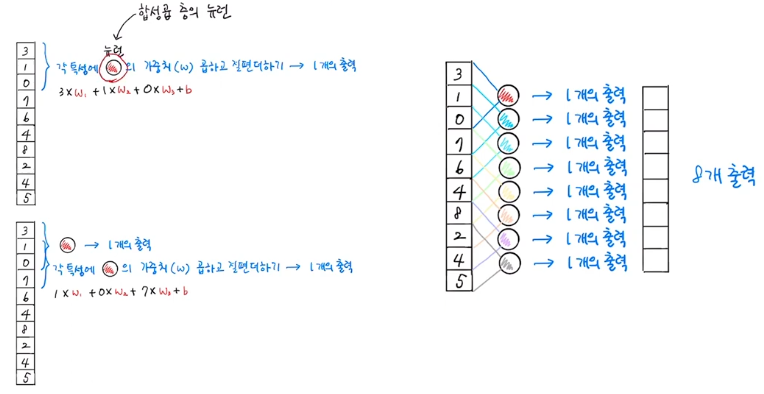
- 각 특성에 뉴런의 가중치를 곱하고 절편을 더하여 1개의 출력을 만들었다.

- 합성곱
- 보통 3~5개의 가중치를 사용한다.
- 가중치 3개에 절편이 1개라면 0~2의 범위에 있는 3개의 특성에 뉴런(합성곱 층의 뉴런)의 가중치(w)를 곱하여 절편을 더하면 1개의 출력이 나온다. 만약 10개의 특성이 있다면 총 8개의 출력이 나온다.
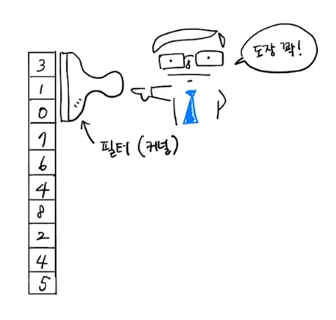
- 커널 = 필터 = 가중치
- 필터에 있는 가중치가 커널이다 라고 표현한다.
- 2차원 합성곱은 커널의 사이즈가 슬라이딩하며 이동된다.
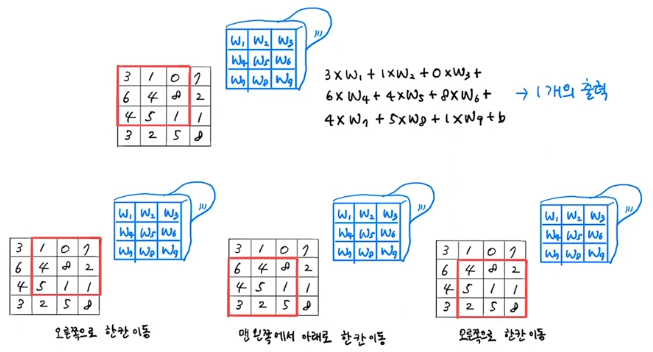
- 2차원 합성곱
- 커널의 이동은 왼쪽 상단에서 오른쪽으로 이동하고 끝에 도달하면 맨 왼쪽 아래로 한 칸 이동하여 오른쪽으로 다시 이동하며 작업을 수행한다.
- 합성곱은 사용하는 2차원 이미지를 그대로 사용할 수 있다.
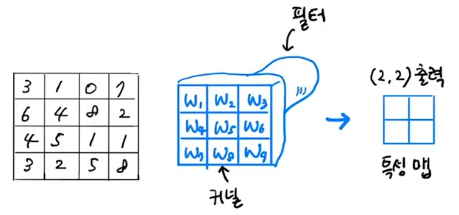
- 특성맵
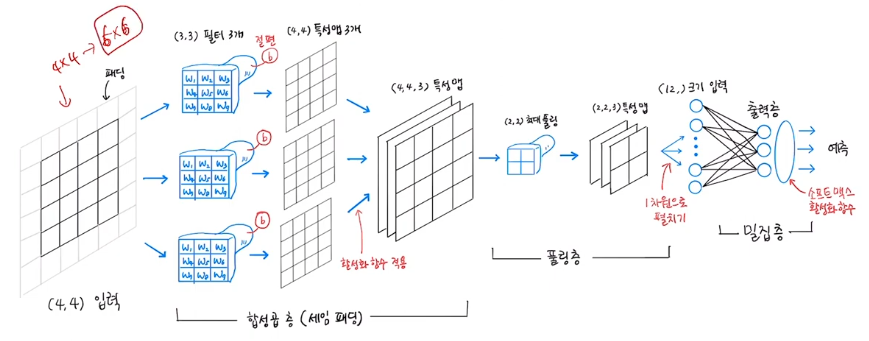
- 만약 4 x 4로 되어 있는 이차원 이미지가 있다면, 3 x 3 커널을 이용해 2 x 2 출력을 만들어 낼 수 있다.
- 이때 만들어지는 출력을 특성 맵이라고 한다.
- 커널이 동작할 때마다 활성화 함수가 적용 된다.
- 합성곱은 2차원 입력이면 2차원 출력을 만들어 낸다.
- 여러 개의 필터
- 뉴런을 여러개 사용하듯 필터도 여러개 사용할 수 있다.
- 필터가 여러 개라면 가중치도 각각 다르다.
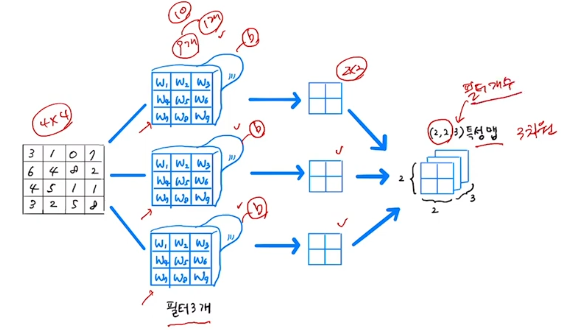
- 만약 4 x 4 사이즈 인풋에 3 x 3 필터 3개를 사용한다면 출력은 2 x 2 출력이 3개 나온다.
- 출력에 대한 표현은 (2,2,3)으로 한다.
- 특성맵의 마지막 차원은 필터의 개수와 같다.
- 케라스 합성곱 층
- 커널의 사이즈는 (3,3), (5,5)를 주로 사용한다.
- 아래 코드는 10개의 필터, 3 x 3의 사이즈, 활성화 함수는 relu를 사용한다.
from tensorflow import keras
# 필터가 10개이며 3x3사이즈이다.
kears.layers.Conv2D(10, kernel_size=(3,3), activation='relu')
- 패딩
- 필터를 사용하면 인풋의 사이즈가 작아진다.
- 패딩으로 0의 값을 이미지 주변에 둘러싸게 되면 사이즈의 크기를 임의로 크게 만들 수 있다.
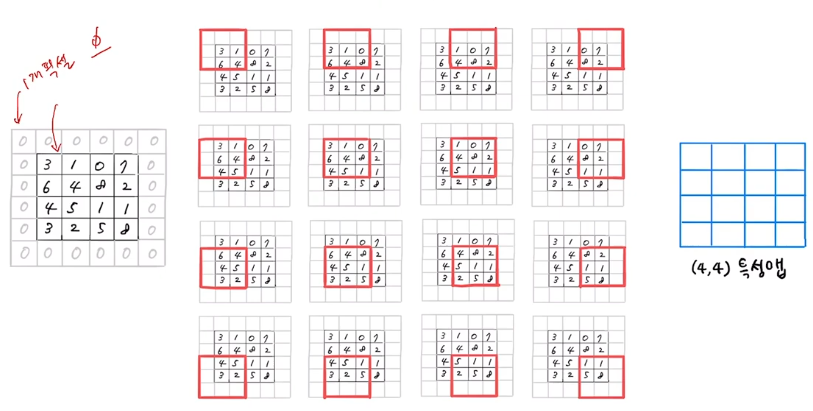
- 4 x 4의 이미지에 패딩을 주면 6 x 6 이미지가 되어 3 x 3의 커널로 인해 4 x 4 아웃풋을 만들 수 있다.
- 입력과 출력 특성형식(4 x 4)이 같다.
- 패딩을 사용하지 않으면 4 x 4 이미지에 3 x 3 커널을 사용할 경우 각 픽셀의 참여도 보다 패딩을 사용할 경우 각 픽셀의 참여도는 증가하게 되어 합성곱 연산의 기여도를 증가시킬 수 있다.

- 케라스 패딩 설정
- padding에 valid를 정의하면 패딩을 사용하지 않는 기본 값으로만 학습하게 된다.
keras.layers.Conv2D(10, kernel_size=(3,3), activation='relu', padding='same')
- 스트라이드
- 커널이 옆으로 이동할 때 얼마만큼의 폭으로 이동할 것인지를 정의한다.
- 4 x 4 크기의 인풋에 패딩을 선언하고 스트라이드를 2로 정의하면 특성맵의 크기는 2 x 2가 된다.
- 기본 1로 정의되어 있다.
keras.layers.Conv2D(10, kernel_size=(3,3), activation='relu', padding='same', strides=1)
- 풀링
- 합성곱층은 입력과 특성맵의 크기를 동일하게 만드는 same 패딩을 많이 사용한다.
- 풀링층은 특성맵의 크기를 절반으로 줄인다.
- 평균 풀링과 최대 풀링을 많이 사용한다.
- 풀링 연산을 할 때 가중치를 사용하는 연산이 아니라 일반 평균 연산을 수행한다.
- 풀링은 특성맵의 크기만 줄이지 채널 차원은 변경하지 않는다.
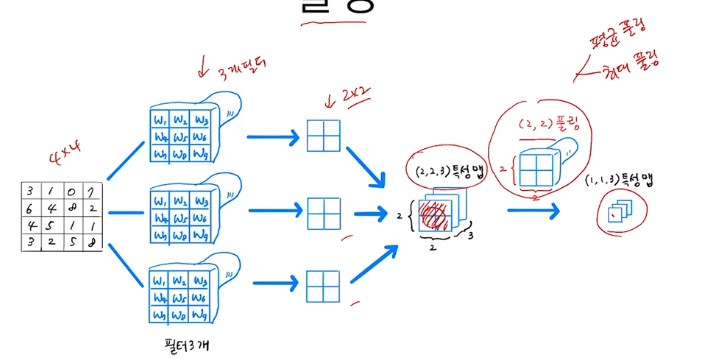
- 만약 4 x 4 입력을 3개의 필터를 사용하면 2 x 2의 특성맵 3개가 만들어진다. (2,2,3)
- 이것을 2 x 2 크기로 풀링을 하면 (1,1,3)의 특성맵이 만들어 진다.
- 여기에서 마지막 3을 채널차원이라 한다.
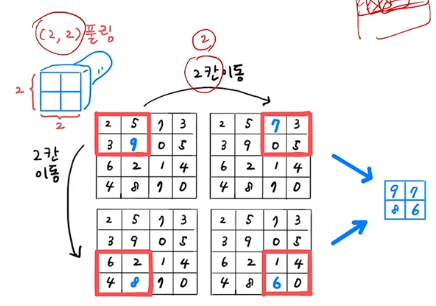
- 풀링의 이동은 특성 간 겹쳐지는 일이 없도록 이동한다.
- 케라스에서 풀링 층은 다음과 같이 선언한다.
- strides는 풀링 크기에 따라 자동으로 정의되기에 따로 만질 필요가 없다.
# 풀링 크기 지정
keras.layers.MaxPooling2D(2)
# strides와 padding은 생략해도 된다.
keras.layers.MaxPooling2D(2, strides=2, padding='valid')
- 합성곱 신경망
- 풀링층을 거쳐 줄여진 특성맵은 다시 밀집층으로 변환되어 학습에 사용된다.
- 합성곱층이 여러 번 반복할 수 있고 합성곱과 풀링층이 하나의 그룹으로 계속 반복될 수도 있다.
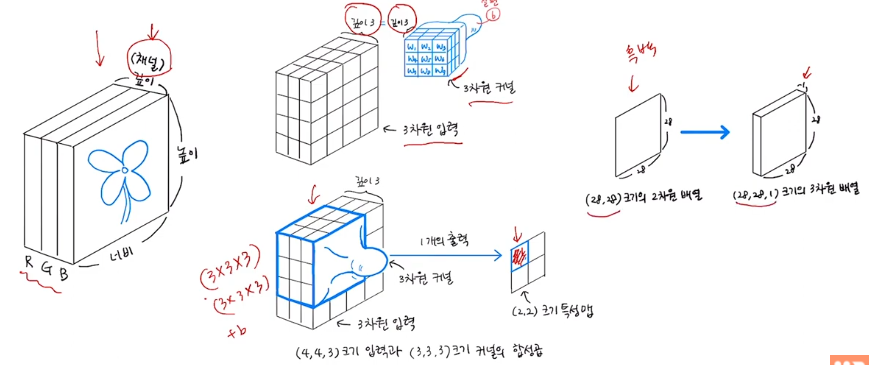
- 3차원 합성곱
- 2차원의 처리 과정과 동일하다 다만 입력값의 깊이만큼 커널의 깊이가 존재하게 된다는 차이가 있다.
- 예를 들이 깊이가 3인 3차원 입력값이 있다면 커널 또한 깊이가 3인 3차원 커널이 된다.
- 3차원 커널을 통해 만들어지는 결과 값은 1개의 특성맵이 된다.
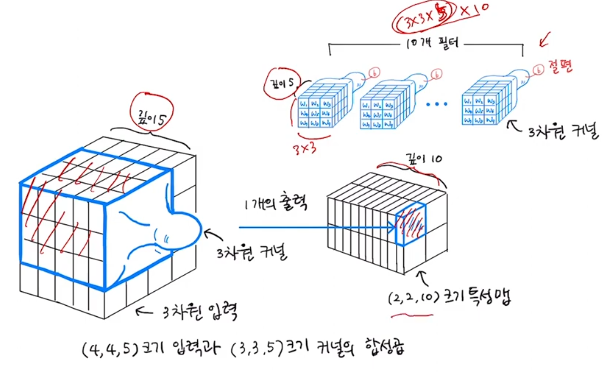
- 여러 개의 필터가 있는 3차원 합성곱
- 깊이가 같은 필터를 사용하여 2차원 합성곱과 같이 처리를 하게 된다.
- reference :
20강 합성곱 신경망의 개념과 동작 원리 배우기
이 글은 https://www.youtube.com/watch?v=tPLRox0YYc8&list=PLJN246lAkhQjoU0C4v8FgtbjOIXxSs_4Q&index=20 보고 공부한 글 입니다. 밀집층(dense층) 1차원으로 펼처진 특성 뉴런은 입력의 갯수와 같다. 도장을 찍듯이 이미지
wonin.tistory.com
[혼자 공부하는 머신러닝+딥러닝] #7 합성곱 신경망
합성곱 신경망을 알아보자.
velog.io

댓글